Cálculos básicos de Volatilidad

Características principales y cálculo

La volatilidad mide la variabilidad de los rendimientos o dispersión de la evolución de una variable respecto de su tendencia central

La variabilidad de los rendimientos de un activo puede resumirse por distribuciones estadísticas. La desviación estándar suele usarse como medida de volatilidad. Con distribuciones normales, la variable aleatoria tiene:

–El 68% de los valores dentro del rango +/- 1 desviación estándar (s)

–El 95% de los valores dentro del rango +/- 2 desviaciones estándar (2s)

–El 99% de los valores dentro del rango +/- 3 desviación estándar (3s)

La no-normalidad de la distribuciones es habitual en las series financieras: Exceso de kurtosis (“colas gordas”/”fat tails”) y skewness. Se expresa en términos anuales.

Para la medida de la volatilidad, es necesario que la media de la variable sea estable (estacionaria). Para evitar el efecto de la tendencia, no se usan los precios sino los rendimientos. Los rendimientos pueden ser calculados de forma discreta o continua:

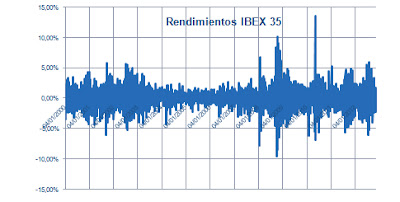
Fijaros por ejemplo en estas dos series. La azul es el IBEX 35 y la roja el IBEX MEDCAP, podemos apreciar claramente como el IBEX 35 tiene una volatilidad más elevada:

La volatilidad tiene características especiales, entre las cuales podemos destacar:

•Persistencia.- Esta característica a veces es conocida como el efecto “memoria”. Se manifiesta en la autocorrelación.

•Clusters.- Los días de altos/bajos rendimientos tienden a estar agrupados.

•Asimetría.- En los mercados de renta variable es especialmente fuerte, el impacto de los retornos sobre la volatilidad es más fuerte en mercados bajistas que alcistas.

•¿Reversión a la media?.- La experiencia indica que las volatilidades suelen revertir a la volatilidad a largo plazo (incondicional).

En el siguiente gráfico podemos apreciar claramente lo expuesto anteriormente. Se ve claramente como en periodos alcistas los rendimientos son más pequeños y en periodos bajistas aumentan.

Una vez vistas todas las características de la volatilidad, vamos a ver cómo se calcula.

Su fórmula:

La fórmula resta a cada rendimiento su rendimiento medio, es decir, la distancia. El rendimiento medio en series financieras es habitualmente muy cercano a cero, de hecho, fijaros en los gráficos anteriores y veréis como hay días de rendimientos positivos y otros negativos, esto hace que en media estén cercano a cero. Bueno, pues la fórmula lo que hace es sumar todas esas distancias y dividirlo por la cantidad de datos para hallar la distancia promedio. Como hay "distancias" positivas y negativas, al sumarlas se compensarían, por eso se eleva al cuadrado, pero como el resultado estaría expresado en puntos porcentuales al cuadrado y sería casi imposible interpretarlos por eso se hace la raíz cuadrada. Se divide por la cantidad de datos menos 1. Es decir utilizamos una media muestral (la media de una muestra) en vez de la media poblacional (media de toda la población). Personalmente, creo que en este caso dividir entre N-1 ó N no aporta gran cosa (que algo dé 19,50% o 19,60% no considero muy relevante, lo importante es saber interpretarlo), pero estadísticamente hablando, una es una estimación más robusta y la otra es máximo verosímil. Lo vais a ver en muchos sitios de cualquiera de las dos maneras (de hecho, ya veréis luego como para calcular un GARCH dividimos por N).

Por otro lado, si he utilizado datos diarios, la volatilidad será diaria. Habitualmente la volatilidad se expresa en términos anuales, por eso habría que anualizarla. Para ello multiplicamos por la raíz de t.

t suele ser 252, ya que  son los días hábiles del año. La raíz de 252 es casi 16 por eso habitualmente para hacer el cálculo "a ojo" se suele utilizar la regla del 16.

Volatilidad Anual	Volatilidad Diaria
16%	1%
24%	1,5%
32%	2%
40%	2,5%

Así, una volatilidad diaria del 1% anualmente es del 16% y si es del 2% pues anualmente del 32%. También es muy útil hacer el proceso inverso, por ejemplo si la volatilidad implícita de una determinada opción está cotizando en un 24%, es que el "mercado" espera que entre hoy y la fecha de vencimiento el activo se mueva una media de 1,5% diario... si piensas que se va a mover más la volatilidad está barata y viceversa.

Cálculo de Simple Moving Average (SMA)

De los gráficos históricos anteriores deducimos que no tiene mucho sentido hacer un cálculo histórico de la volatilidad para tomar alguna decisión en el mercado. Hay periodos de mucha volatilidad y periodos de baja volatilidad, hacer un cálculo con muchísimos datos hace una especie de media de todo el periodo, lo cual no es muy útil si lo que quiero es saber o estimar como se va a comportar por ejemplo mi cartera en los próximos días. La pregunta es ¿se va a comportar mi cartera/activo como lo ha hecho de media los últimos 12 años? puede que lo haga, nunca se sabe, pero lo más lógico es pensar que en ausencia de nuevos "shocks" los próximos días se va comportar como lo ha venido haciendo últimamente.

La volatilidad va aumentando y disminuyendo como hemos visto que le pasa a los rendimientos, para intentar capturar la dinámica de la volatilidad se suelen utilizar muchos métodos, el más sencillo y potente son las medias móviles simples.

La desviación típica calculada cada t días (ventana temporal). Cuanto más pequeña sea la ventana temporal más sensible será la volatilidad. Cada dato tiene la misma importancia dentro de la ventana temporal, por ello si hay un dato (rendimiento) muy grande, cuanto más grande sea la ventana temporal más diluido quedará y por tanto no reaccionará tanto la volatilidad.

El razonamiento de este método está que nos fijaremos en que si queremos saber cómo se comportará la volatilidad, por ejemplo, en los próximos 6 meses sería razonable pensar que salvo que ocurra algún imprevisto o dato relevante, la volatilidad se comportará más o menos como en los últimos 6 meses.

Normalmente: a 1 mes, 3 meses, 6 meses, 9 meses y un año.
En la siguiente gráfica podéis ver la diferencia entre una media móvil a 20 días y a 60 días. La de 20 días reacciona mucho antes ante incrementos/disminuciones en el tamaño de los rendimientos que la de 60 días. El cruce de medias como siempre es un indicador cambio de tendencia, y por lo tanto también puede usarse para tomar decisiones sobre volatilidad.

La volatilidad histórica calculada por medio de medias móviles, permite crear los llamados “Conos” de volatilidad que son una herramienta muy útil para hacerse una idea de los niveles actuales de volatilidad comparándolos con los niveles históricos y así, poder tomar decisiones en cuanto a la volatilidad futura.

De las distintas ventanas temporales, se calculan varios percentiles. Si se ordenasen los datos de menos a mayor, el percentil 0% es el dato más pequeño y el 100% es el máximo. El percentil 50% es justo el del medio, el que dejan el 50% de los datos por debajo de él. 

Si se grafica la tabla anterior, tenemos el cono de volatilidad.

Otros estimadores de volatilidad:

Hasta ahora, en todas las fórmulas anteriores, hemos usado los datos de cierre (close-close), llamado estimador CC.

Otra clase de estimador (HL) usa intraperiodos altos y bajos para caracterizar la distribución. Según muchos autores, estos estimadores de valores extremos son más eficientes porque usan información adicional acerca de los movimientos a través de un periodo en el cual si tomamos sólo el último dato no recogemos dicha información. Los pioneros en esta área fueron Parkinson (1980) y Garman-Klass (1980):

A favor de estos modelos:
• Con un número de 5 a 7 veces menor de datos se obtienen estimaciones estadísticamente igual de precisas que con el modelo CC.
•Los estimadores de valores extremos son temporalmente más estables

Garman-Klass utiliza adicionalmente el precio de cierre y apertura, pero no hay grandes diferencias con Parkinson como puede apreciarse en el siguiente gráfico:

Volatilidad condicional (Heteroscedástica)

Una manera de capturar las características dinámicas de la volatilidad es usar una media móvil exponencial de las observaciones históricas donde las últimas observaciones tienen un mayor peso en la estimación de la volatilidad. Este método tiene dos importantes ventajas sobre el método explicado anteriormente de medias móviles simples (Equally Wighted Model) en el que cada dato tiene las misma importancia dentro de la ventana temporal:

La volatilidad reacciona más rápido ante los “shocks” del mercado, ya que los datos más recientes tienen una mayor relevancia que los datos más distantes.

Normalmente, después de un “shock” de mercado (rendimiento muy grande positivo o negativo) la volatilidad cae cuando el peso del “shock” cae. A diferencia de esto, en el modelo de medias móviles simples, el “shock” causará un aumento paulatino de la volatilidad que seguiremos “arrastrando” hasta que salga de la ventana temporal, lo que quiere decir que un dato muy grande de un solo día podría aumentarnos la volatilidad durante meses.

ARCH (Auto Regressive Conditional Heteroscedasticity). Engle (1982)

La volatilidad histórica como hemos calculado antes:

Un cambio que se suele hacer a la fórmula anteriormente expuesta es:
•Asumir que el rendimiento medio es 0 (casi verdad)
•N-1 se reemplaza por N que nos cambia de una estimación insesgada a otra de Máxima Verosimilitud.

La ecuación anterior, da el mismo peso a cada dato, para monitorizar el nivel actual de volatilidad, quizá sería más apropiado dar más peso a los datos más recientes, siendo la suma de todos los pesos igual a 1:



Una extensión de esta idea, es que el modelo asume que hay una varianza incondicional, también llamada a largo plazo (V) , a la cual también hay que dar un peso dentro de la ecuación:



GARCH (Generalized Auto Regressive Conditional Heteroscedasticity). Bollerslev (1986)
Una generalización del modelo anterior:



La generalización del modelo ARCH, proceso AR (q), llamado GARCH, proceso ARMA (p, q), tiene un componente autoregresivo y de media móvil en la varianza heteroscedástica. La ventaja sobre el modelo ARCH es que te tiene más parsimonia, representación que es más fácil de presentar y estimar.
Los parámetros que utilizamos para estimar los modelos GARCH, se pueden construir maximizando la función de Máxima Verosimilitud. Normalmente, se asume que los residuos siguen una distribución normal y son independientes (IID). Los residuos son:




La optimización maximiza el logaritmo de la función de máxima verosimilitud, ignorando los factores multiplicativos constantes queda:



El modelo GARCH, puede se usarse para extrapolar la volatilidad a un periodo de tiempo. El método de multiplicar la volatilidad por las raíz del tiempo sólo funcionará si el valor inicial es la varianza incondicional, si fuera mayor sobrevaloraría y si fuera inferior infravaloraría.


A continuación vemos el gráfico de la volatilidad GARCH para el IBEX 35 

Los parámetros que yo he utilizado han sido:

Este es un modelo muy utilizado en la gestión de riesgos y más concretamente en el cálculo del VaR porque ajusta muy bien el riesgo.

Si bien es cierto que como veremos posteriormente, tiene en cuenta la reversión a la media, lo cual puede no aplicar de la misma manera a todos los productos y por eso también se utiliza el modelo EWMA que vamos a ver a continuación y que es igual que GARCH pero sin reversión a la media.

Alisado Exponencial: EWMA (Exponentially Weighted Moving Average). Riskmetrics

EWMA depende del parámetro l (0<l<1) que se llama “Decay Factor”.

Este parámetro determina los pesos relativos que son aplicados a cada observación (rendimientos): 

Si l =1 cada observación tendría el mismo peso (equally weigthed) 

Cuanto más cercano a 0 sea el factor quiere decir que más importancia se le da a los últimos datos y olvidamos antes los datos pasados. 

Riskmetrics recomienda: 

l= 0.94 para datos diarios

l= 0.97 para datos mensuales

Por ejemplo, veamos una comparativa entre una volatilidad calculada con pesos iguales para todos los rendimientos y una volatilidad EWMA donde los pesos son asignados exponencialmente:

Mientras que el SME aplica el mismo peso para todos los datos (5%), en EWMA el peso sobre los datos va variando (1.9% a 6%), teniendo mayor peso los datos más recientes.

Una característica que hace muy atractivo al modelo de pesos exponenciales es que puede ser escrito de forma recursiva y así ser usado como base para hacer estimaciones de volatilidad. A pesar de la sofisticación que representa frente al modelo de medias móviles simples, es muy fácil de implementar.

Si asumimos que la media es cero podemos dar la predicción de volatilidad del periodo t+1 con los datos en el periodo t (un día antes):

A pesar de que Riskmetrics recomienda unos l en función de los datos, nosotros podremos estimar el l que más se adecue a nuestros datos. Uno de los criterios para estimar l es el de la Raíz del Error Cuadrático Medio (RMSE):

Fijaros en el siguiente gráfico cómo la asignación de pesos exponencial hace un efecto parecido al de una ventana temporal. Por ejemplo para un l del 0,94, el 99% del peso está en los último 74 datos.

Si comparásemos un GARCH con un EWMA:

Fijaros cómo se parecen bastante, pero al GARCH,  esa reversión a la media le hace de efecto "imán" no le deja bajar ni subir tanto como lo hace EWMA, que tiene total libertad.

GARCH vs EWMA

El modelo EWMA es un caso particular del GARCH donde:

Por lo tanto, GARCH y EWMA son modelos muy similares excepto por el hecho de que el GARCH además de asignar pesos que decaen exponencialmente a los rendimientos al cuadrado  pasados, también asigna algo de peso a la varianza incondicional (volatilidad a largo plazo).

Cuando en el GARCH el mejor valor que podamos estimar a w es cero, el modelo se reduce al EWMA, pero en las circunstancias en las que el mejor ajuste sea negativo, el GARCH (1,1) no sería estable y deberíamos cambiar al EWMA. Aunque utilizando Solver de Excel® no es complicado estimar los parámetros de un GARCH (v, a y b), el EWMA es muy simple ya que sólo hay que estimar un parámetro ( l). 

Como ya hemos comentado antes, en periodos largos, EWMA y GARCH son algo diferentes, ya que GARCH tiene reversión a la media y EWMA no (El parámetro de persistencia  a+b en EWMA es 1, mientras que en GARCH es menor que 1, normalmente alrededor de 0.95), por eso  l es diferente según se tomen los datos diarios o mensuales.

Depués de ver todos estos modelos "tan sofisticados", me gustaría poneros un gráfico dónde comparamos la volatilidad EWMA y la volatilidad histórica con ventana temporal de 20 días para que veáis como la sofisticación no aporta gran cosa para la toma de decisiones para el común de los mortales, salvo en determinados casos, claro está, que sí necesitan algo más que un HV20 "mondo y lirondo"

En el siguiente gráfico, una comparativa de todos los modelos que hemos comentado, como veis tienen un comportamiento bastante parecido.

Volatilidad Implícita

Es uno de los parámetros con mayor peso dentro de la valoración de Opciones. La volatilidad afecta igualmente a Call y a Put, provocando aumentos de sus primas si ésta aumenta y viceversa.

Por tanto, compradores de Opciones se benefician de aumentos de volatilidad implícita y los vendedores de disminuciones.

Para calcular la prima de una opción, los parámetros que se necesitan son:

                                            Prima = P(PS, PE, t, σ, r, d)

siendo,

PS : precio activo subyacente

PE : precio de ejercicio

t : tiempo de vida que tiene la opción, normalmente en años. Por ejemplo 6 meses son 0,5 años.

σ : volatilidad del activo hasta la fecha de vencimiento

r : tasa de interés libre de riesgo a la que se puede invertir hasta la fecha de vencimiento.

d : dividendos. La familia de modelos de valoración Black-Scholes (habría que añadir a Merton para ser justos) utiliza formato continuo, es decir una compañía paga por ejemplo un 5% en dividendos todos los días del año "paga un poquito". El modelo de valoración binomial (Cox-Ross-Rubinstein) utiliza fecha exacta del pago y cantidad.

 En principio, todos los parámetros anteriores son conocidos o fácilmente estimables (dividendos en el corto plazo, en largo no), excepto la volatilidad.

Como habéis visto, anteriormente he subrayado que el parámetro que hay que utilizar para calcular la prima es la volatilidad del activo hasta la fecha de vencimiento, es decir, la volatilidad futura. ¿Cómo sabemos qué volatilidad va a tener el activo subyacente?, no se sabe, se intenta estimar.

Primero intentamos ver qué ha hecho la volatilidad en el pasado reciente, es decir, calculamos la volatilidad histórica. ¿Qué volatilidad utilizamos? ¿EWMA, Parkinson, Garman-Klass, SMA? Si pedimos a 10 personas la volatilidad esperada de un activo para calcular sus opciones, podría suceder que tuviéramos 10 datos distintos, todos ellos igualmente “buenos” a priori. Ésta es la principal crítica, entre otras,  que reciben los modelos de valoración de opciones tradicionales.

veamos un ejemplo,

Cálculo Prima: MIX

PS : precio activo subyacente 14734

PE : precio de ejercicio 14750

t : tiempo de vida que tiene la opción 85 días

σ : volatilidad (18,26% calculado con EWMA)

r : tasa de interés libre de riesgo 4.13%

d : dividendos No Hay

                  Prima = 505.23

La volatilidad implícita es la volatilidad con la que están cotizando las opciones en el mercado, la que despejamo0s del modelo de valoración. Siguiendo con el ejemplo anterior,  si acudo al mercado y veo que las opciones se están negociando a 510.57 ¿qué pasa?

PS : precio activo subyacente 14734

PE : precio de ejercicio 14750

t : tiempo de vida que tiene la opción 85 días (21/09/2007)

σ : volatilidad ESTA ES PRECISAMENTE LA INCÓGNITA. SI DEPEJAMOS NOS DA 18.45%

r : tasa de interés libre de riesgo 4.13%

d : dividendos No Hay

                Volatilidad implícita = 18.45%

La Volatilidad Implícita, aparece asociada a cada contrato de opción más que al Activo Subyacente. Se obtiene a partir de las primas de las opciones negociadas en el mercado. 

Es un factor muy ambiguo que se obtiene despejando de las fórmulas de valoración de opciones. Se llama implícita, porque el precio de las opciones refleja expectativas sobre la volatilidad del activo subyacente sobre un periodo cierto de tiempo.

Como se puede observar en el gráfico anterior donde están representadas la volatilidad histórica a 20 días y la volatilidad implícita de la opción ATM también a 20 días del IBEX 35 (ya veremos un poco más adelante como para conseguir una referencia contante a 20 días habrá que interpolar la volatilidad implícita de la ATM de primer y segundo vencimiento). Observad como la volatilidad implícita y la histórica se siguen bastante bien, aunque la volatilidad implícita es un poco menos brusca en su oscilación. Otra característica que se observa muy bien el gráfico y que es básica a la hora de invertir en volatilidad es que la volatilidad implícita en términos generales suele estar por encima de la histórica, esa diferencia se llama "volatility premiun" o prima de volatilidad y se explica por la incertidumbre que existe, la gente está dispuesta a pagar un poco más de volatilidad de lo que debiera por comprar opciones y poder cubrirse o limitar pérdidas, depende de la estrategia.

Aunque la referencia sea la volatilidad de las opciones ATM, no todas las series de opciones de igual vencimiento negociadas en el mercado, incorporan una misma volatilidad implícita; la función que relaciona los distintos Precios de Ejercicio con sus correspondientes volatilidades se denomina SKEW DE VOLATILIDAD

SKEW DE VOLATILIDAD

Si analizamos la volatilidad implícita de las opciones de un mismo vencimiento, observamos que estas varían según los distintos precios de ejercicio.

Los operadores toman como referencia la volatilidad de las opciones ATM. La unión de esas variaciones de las volatilidades en cada precio de ejercicio con respecto a la de la opción ATM se conoce como curva skew de volatilidad.

Los distintos mercados presentan skews de volatilidad “típicos” diferentes, que a su vez pueden variar en un mismo mercado según la situación del mismo. Esta variación incorpora un riesgo adicional a la operativa con opciones: riesgo de skew de volatilidad.

Skew normal o smile: Característico de los mercados de deuda y divisa.

Skew decreciente: Característico de los productosde oferta. Fundamentalmente Renta Variable. 

Skew creciente: Característico de los productos de demanda. FundamentalmenteCommodities.

Cada Precio de ejercicio tiene una volatilidad asociada distinta. Esto no quiere  decir que sea más volátil una opción de precio de ejercicio bajo que otra de strike más alto. La volatilidad se refiere al activo subyacente, lo que ocurre es que no se valorará de la misma manera una opción que otra y habrá opciones a las que se le atribuye una mayor prima de riesgo que se traslada al precio por medio de la volatilidad.

¿qué es más probable alcanzar más rápidamente? La evidencia empírica del mercado nos dice que cuando sube el mercado lo suele hacer despacio y cuando cae lo hace muy rápidamente (efecto pánico), luego es más probable alcanzar antes el precio de ejercicio 14500, y si esto ocurre la volatilidad habrá aumentado seguramente, por ello los operadores le dan una mayor prima de riesgo a estos precios de ejercicio más bajos. Por ejemplo, imaginad que un Put muy fuera del dinero (OTM) valorado con la misma volatilidad que la opción ATM tiene un precio de 0,04, aunque esta opción es muy poco sensible (tiene una delta muy baja), una caída drástica del subyacente podría hacer que su prima fuera 0,08 y por tanto el vendedor de esta opción podría perder muchísimo dinero. Una manera de trasladar este riesgo al precio es aumentarle la volatilidad de tal manera que la opción sea más cara. ¿cuánto más cara? la respuesta es bien sencilla, lo que esté dispuesto a pagar el comprador.

No existe un fórmula para determinar el skew de volatilidad, ya que es el resultado de la oferta y la demanda. El vendedor de opciones querrá vender con volatilidades altas y comprador querrá comprar con volatilidades bajas.

Los operadores colocan los precios de las opciones para los distintos precios de ejercicio en función de sus expectativas sobre la volatilidad, la oferta y la demanda llegarán a un acuerdo sobre la volatilidad que tiene cada uno de estos.

Normalmente, aunque no siempre (aquí no hay reglas fijas que siempre valgan), en los mercados de Renta Variable, el skew suele ser decreciente, muchos inversores estarán largos de activo subyacente y venderán Call (venta sintética de put) fuera del dinero en mercados alcistas para arañar rentabilidad extra (generación de Alpha) o comprarán Put también fuera del dinero cunado piensan que el mercado va a caer y quieren proteger sus inversiones. A veces toman ambas posiciones para crear un Bull Spread.

La demanda de Puts OTM y la oferta de Call OTM crea esta forma decreciente:

En "argot" de mercado al lado de la curva de skew de precios de ejercicio por debajo del ATM se llama lado PUT, mientras que a los precios de ejercicio superiores se les denomina lado CALL.

Riesgo de SKEW

Unos de los riesgos a tener muy en cuenta cuando utilizamos opciones es el riesgo de Skew, sobre todo cuando utilizamos Estrategias de Volatilidad. El riesgo será mayor cuanto más OTM o ITM estén las Opciones (las OTM al no tener valor intrínseco y ser casi cero serán muy sensibles a cambios en volatilidad y Skew).

Estructura Temporal

Las opciones sobre un mismo subyacente y mismo strike pero de distinto vencimiento, tienen diferentes volatilidades implícitas. A esto se denomina “estructura temporal”.

Los vencimientos más alejados, suelen tener volatilidad superior por tener el activo subyacente mayor tiempo para fluctuar, pero esto no siempre es así, depende del mercado, el producto y el momento..

Se suelen producir movimientos más fuertes en los vencimientos cercanos que en los lejanos (esto también depende del mercado, el producto y el momento):

• La volatilidad de un vencimiento lejano es más incierta y por tanto más estable (más tiempo para revertir a la media).
• La liquidez es mayor en los vencimientos cercanos.

Si combinamos el skew de un activo y su estructura temporal, obtendremos lo que se denomina “superficie de volatilidad”.

La superficie de volatilidad permite hacer un análisis mediante el cual podemos estimar la dinámica del cambio de la volatilidad a lo largo de los strikes y de los distintos vencimientos.

Veamos algunos ejemplos, aquí tenéis una superficie de volatilidad hecha en Excel con precios en tiempo real. Como podéis ver tiene un aspecto en general decreciente, sin embargo no se cumplen muchas de las cosas que hemos comentado anteriormente. Fijaros en los Call OTM de primer vencimiento, ¡¡aumenta la volatilidad!! que ocurría en ese momento es que la gente quería sustituir las acciones de este activo por Call fuera del dinero y esa demanda hizo subir la volatilidad.

Más ejemplos de superficie de volatilidad, gráficos sacados de Bloomberg. Hay un cuadro con la superficie por Strike y otro por Moneyness. El Moneyess se suele utilizar para no tener que cambiar la volatilidad de los Strikes constantemente (modelos Stiky-Strike y Stiky-Delta)  y por eso a la opción ATM se le denomina 100%, un precio de ejercicio un 10% por debajo sería una opción 90% mientras que un precios de ejercicio un 10% por encima sería una opción 110%.

INTERPOLACIÓN DE LA  SUPERFICE VOLATILIDAD

Para cualquier operador del mercado de opciones, resulta básico determinar la superficie de volatilidad del mercado. Como hemos comentado anteriormente, la volatilidad implícita se despeja de los modelos de valoración de opciones una vez conocemos cual es la cotización de la prima. Si hacemos esto para todas las opciones cotizadas en el mercado, tendremos las volatilidades a las que se cotiza cada precio de ejercicio en un determinado momento y podremos determinar cuál es la función que los relaciona. Así, si fuera un trader de volatilidad y  me piden cotización para unas opciones que no estén cotizadas, podré determinar cuál es la volatilidad con la que debiera cotizar.

En base a lo anterior se pueden dar dos tipos de situaciones:

• Determinar un precio de ejercicio intermedio. No suele darse este problema, pero tiene fácil solución. Por ejemplo, si me piden cotizar la opción 110 porque no cotiza en el mercado, pero sí lo hacen la opción 105 y 115, podré determinar el nivel de volatilidad.
• Determinar un precio de ejercicio muy fuera del dinero (o dentro) no intermedio. Éste sí puede ser un problema. Por ejemplo, me piden cotizar una opción 60% cuando en el mercado la opción más alejada de ATM que cotiza es un 80%.

Existen varios modelos para hacer esto que son más o menos matemáticos, pero lo realmente importante es que todo reside en la liquidez del mercado.

Modelo Lineal

Este es el modelo empleado por MEFF para dar las volatilidades de cierre de las opciones. Es un modelo muy sencillo y algo simplista, pero para la realidad del mercado español va perfecto. Este modelo, como podemos apreciar en el siguiente gráfico, ofrece dos pendientes: una para los precios de ejercicio superiores y otra para los inferiores.

Tal y como hemos visto anteriormente, la volatilidad implícita se calcula despejando la volatilidad a partir de las primas cotizadas en el mercado. Para ello según el tipo de opción hay que utilizar el modelo adecuado:

Para opciones europeas: en general las suelen serlo las opciones sobre índice, en nuestro caso, en MEFF, lo son las opciones sobre IBEX y opciones sobre acciones. Se utiliza el modelo Black-76 que es una pequeña modificación en el modelo Black-Scholes para cuando el subyacente es un futuro. Los futuros ya incorporan los tipos de interés y dividendos por lo que es muy sencillo:

Para opciones americanas: en general suelen serlo las opciones sobre acciones. En el caso español en opciones sobre acciones tenemos de los dos tipos americanas y europeas. Tradicionalmente han sido siempre americanas y hace unos pocos años que se introdujeron las europeas.

Pues bien, el modelo lineal en primer lugar  lo que se hace es despejar la volatilidad implícita a partir de las primas de mercado.

En el ejemplo que os pongo a continuación, la parte de la derecha es la pantalla dónde cotizan las opciones. Una vez cierra el mercado, de las cotizaciones que tienen los "market makers" se saca el precio medio entre bid-ask y se utiliza como precio teórico y se despeja la volatilidad como vemos en el boletín de cotización de la izda.

En el modelo de valoración se puede introducir la volatilidad y nos da como resultado la prima, pero si conocemos el valor de la prima, podemos obtener la volatilidad implícita.

Una vez despejada la volatilidad implícita de los precios de ejercicio más cercanos al subyacente (por encima y por debajo), se calcula la volatilidad de un precio de ejercicio teórico que es el que llamamos ATM y que es igual al precio del subyacente. El modelo lineal (en MEFF) asume:

• Sólo hay un SKEW UP y un SKEW DOWN.
• Se considera serie ATM el precio del activo subyacente.
• Se aplica una variación de +/- 3% a dicho precio y a continuación se obtiene la diferencia entre los puntos.
• Se calcula la diferencia entre los precios de ejercicio y el ATM.

Para ello se establece la siguiente regla de 3. 

Para precios de Ejercicio Superiores:

Para precios de ejercicio inferiores:

A continuación os pongo un ejemplo:

Otros modelos

Para precios de cierre en un mercado en un mercado no excesivamente profundo, el modelo lineal funciona muy bien, pero para cotización en tiempo real podría no ser suficiente. En el mercado español tenemos subyacentes liquidísimos y otros que no lo son tanto.

Para un "Market Maker" es muy importante tener perfectamente establecidas sus curvas de volatilidad (superficies) en tiempo real, para ello utilizan métodos un poco más sofisticados. Una pantalla de un "Market Maker" podría ser ésta:

No voy a dar toda la explicación matemática de los diferentes métodos de interpolación (aunque haré algún artículo con alguno de ellos para que veáis cómo se calcula), pero sí os pondré un par de pantallazos con dos de los métodos más utilizados.

Este primer pantallazo está hecho con un modelo de interpolación  Cubic Splines o segmentos cúbicos:

En el segundo pantallazo el "wing model" de ORC, que se ha convertido en los últimos años en un estándar en el mercado:

ORC es una casa de software muy utilizado para market making y trading de volatilidad por grandes bancos. Las tres fotos de pantallas anteriores son de este software.

INTERPOLACIÓN DE VOLATILIDAD EN EL TIEMPO (VOLATILIDAD FORWARD)

Debido a que las opciones cotizadas en mercados organizados tienen vencimientos estandarizados, la volatilidad implícita se despeja para cada uno de los vencimientos.

A veces surge la necesidad de saber la volatilidad implícita de una opción con unos días a vencimiento determinados.

Imaginad la siguiente situación:

A las opciones de primer vencimiento le quedan 33 días mientras que a las de segundo vencimiento le quedan 63 días:

Podríamos necesitar saber dos cosas…..:
–La volatilidad implícita a de una opción  con 45 días a vencimiento.
–La volatilidad forward entre el día 33 y el 63 (volatilidad a 30 días dentro de 33 días)

A continuación os pondré cómo se calculan, pero antes un par de avisos importantes:

-La volatilidades hay que pasarlas a varianzas, ya que no es posible la suma de raíces cuadradas.

-A diferencia de lo que hemos hecho anteriormente con las volatilidades históricas, para pasar a anual o a diaria, la volatilidad se multiplica o divide por la raíz de 365 ó 366, ya que son los días reales a vencimiento. Utilizábamos 252 en las volatilidades históricas porque teníamos datos diarios de los días que hay negociación.