CBOE S&P 500 95-110 Collar Index

Hoy os pongo otro índice interesante del CBOE. Lanzado en septiembre de 2008, está  diseñado para ofrecer a los inversores del índice una protección frente a caídas bruscas del mercado. Aunque el nombre sea Collar (también llamado Túnel o Risk Reversal) no es exactamente eso esta estrategia.

El índice consiste en una posición larga en el índice S&P 500 total return y un túnel bajista en el que las opciones tienen diferente vencimiento:

• Una compra de Put un 5% OTM de vencimiento 3 meses.
• Venta de Call de Call un 10% OTM de vencimiento un mes para financiar la compra de las Put.

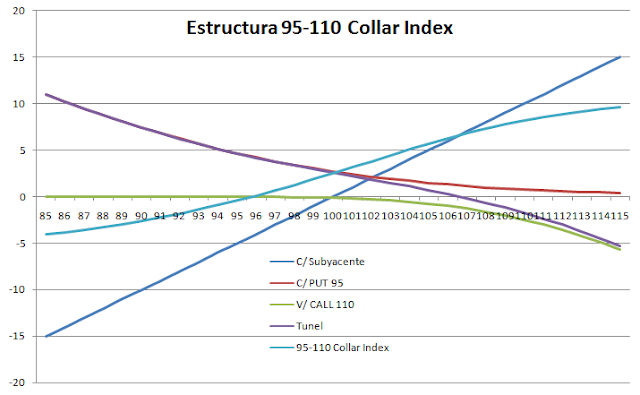
La posición resultante es un “diagonal spread”, un Call Spread pero la opciones son de diferente vencimiento. En el gráfico 1 se muestra con propósitos didácticos, una hipotética situación a vencimiento de todas las opciones para que se identifique claramente la estructura. Ésta no es real, ya que la opciones Call y Put tienen distinto vencimiento. En el gráfico 2 se observaría la misma estructura con las Put a 90 días a vto y las Call con 30 días a Vencimiento. Aunque es más complicado apreciar la estructura, si se puede ver cómo es in índice muy tranquilo, tanto en la subida como en la bajada.

Gráfico 1:hipotética situación a vencimiento de todas las opciones

Gráfico 2:estructura con las Put a 90 días a vto y las Call con 30 días a Vencimiento

En el gráfico 3 se puede apreciar como es un índice con muchísima menos volatilidad (casi la mitad). Al estar limitado con opciones tiene la ventaja de tener protección frente a las pérdidas, pero el inconveniente de estar limitado en los beneficios. Las caídas bruscas le afectan poco, pero como contrapartida, las subidas bruscas también le afectan poco. Para que le vaya bien tiene que subir tranquila y continuadamente.

Grafico 3: comparativa CBOE S&P 500 95-110 Collar Index y SP500 Total Return

Espero que os haya gustado...

CBOE Tail Hedge Index (VXTH)

Hoy os presento otro índice interesante, el CBOE Tail Hedge Index (VXTH). Es un índice diseñado para hacer frente a movimientos extremos del Mercado (Cisnes negros). Mantiene una cartera de S&P500 (índice S&P500 total return) y compra Call de VIX de vencimiento un mes con delta 30 (OTM). 

En cada roll-over varia el peso de los Call en cartera en función de los niveles del futuro de VIX como probabilidad de que ocurra un suceso extremo. Lo hace de la siguiente manera:

Es importante darse cuenta cómo el índice, cuando la volatilidad está alta compra menos cantidad de Call y cuando está muy alta, ya no compra Call.

El poder de este índice radica en el violencia que tiene la volatilidad, cuando ocurre un evento dramático, la volatilidad literalmente explota, beneficiando a los Call, aún siendo una cantidad muy pequeña, se nota.

Os recomiendo que visitéis la página web del CBOE http://www.cboe.com/micro/vxth/ viene mucha información y hasta hojas excel con datos históricos y de cómo se rola el índice. ¡¡Muy interesante!!.

He tenido curiosidad por ver cómo se ha comportado el índice durante el mes de agosto y he hecho un gráfico. En el siguiente gráfico comparo el S&P500 total return (línea roja) y el índice CBOE Tail Hedge Index (VXTH) (línea azul), se puede observar como la diferencia radica en el caso de las caídas extremas de agosto 2015, en el que el índice VXTH cae algo menos. Si pasa tiempo sin esas caídas y el índice se mantiene en un determinado rango, tiene un gasto en opciones Call que compra relativamente caras y que hace que tenga algo menos de rendimiento que el S&P500 total return, de ahí el posterior peor comportamiento relativo. 

Espero que os haga gustado....

CBOE VIX Premium Strategy Index (VPD) y CBOE Capped VIX Premium Strategy Index (VPN)

En los artículos anteriores he estado explicando qué es el VIX, cómo funcionan los futuros, que es un activo con mucha volatilidad, etc..Hay mucha gente que se pregunta cómo se invierte en volatilidad, bien pues los siguientes post que voy a hacer tienen que ver con estrategias que se suelen utilizar e índices que se hacen para medir estas estrategias. Son muy interesantes.

El primero es el CBOE VIX Premium Strategy Index (VPD) y CBOE Capped VIX Premium Strategy Index (VPN).- Miden el rendimiento de una estrategia que consiste en estar en una cuenta de mercado monetario y vender futuro de VIX a un mes. Recordemos que cuando sube el mercado suele bajar la volatilidad y viceversa. Por tanto, vendido de futuro de VIX es equivalente a estar "largo" en renta variable.

Cada vez que rola la posición, solo se invierte el 75% de la posición, para preservar el capital en el caso de una subida repentina de la volatilidad del 25%. La forma de la estructura temporal del futuro es básica para el rendimiento de la estrategia, ya que rolar una posición corta si el mercado está en "Contango" es beneficiosa, el inconveniente es que cuando sube mucho la volatilidad, pierde por estar corto de volatilidad y porque la estructura cambia a "Backwardation", el rolo con la estructura así genera pérdidas. Si no sabes de lo que estoy hablando mira aquí. 

Por lo tanto, este índice ofrece la oportunidad de capturar “Volatility Premium”.La diferencia entre ambas versiones es que la versión “Capped”, limita las pérdidas con la compra de Call de VIX muy OTM.

En el gráfico 1 se muestra el rendimiento de ambos índices desde el año 2004 comparándolos con el rendimiento del S&P500 total return.

Gráfico 1: Comparativa entre los índices CBOE VIX Premium Strategy Index (VPD) y CBOE Capped VIX Premium Strategy Index (VPN) y el S&P500 total return. Elaboración propia a partir de datos de CBOE.

Volatilidad IBEX 35® a 7 de septiembre de 2015

Hola a todos,

Llevo unas cuantas semanas liado con otras cosas y tengo preparados ya los próximos "post" que iba a poner, pero siendo este un blog de volatilidad no puedo obviar lo que está sucediendo estos días en el mercado. 

Como siempre lo primero, os pongo el gráfico y luego os comento un poco....

Ahora mismo estamos en un 32,64% de volatilidad a 20 días y 27,11% de volatilidad a 60 días... la pregunta que muchos os estáis haciendo es ¿es mucho o es poco?, la respuesta es.. depende... ahora os explico.

En el gráfico os he puesto en la linea verde el IBEX 35®, la linea azul es la volatilidad a 20 días y la roja es la volatilidad a 60 días. Fijaros como en periodos alcistas el régimen de volatilidad es bastante inferior al de periodos bajistas. Si consideramos que ha cambiado la tendencia del mercado a bajista (lo cual no digo que no pueda ser.....pero todavía es un poco pronto para poder afirmarlo) podemos ver todavía la volatilidad aumentar mucho más, hasta niveles del 50%. Si por el contrario consideramos que todavía estamos en un mercado alcista, estamos en máximos de volatilidad y necesariamente tiene que bajar.

Qué más información puedo obtener...de la página web de MEFF, visitando su boletín de cotización, puedo obtener muy fácilmente los datos de volatilidad implícita.Os pongo en un gráfico la estructura temporal, para que veáis que está invertida y en otro los Skew de diferentes vencimientos. Lo que nos indica el mercado de opciones, es que ha aumentado a muy corto plazo la volatilidad, pero para vencimientos largos cotizan volatilidades más bajas. Esperan que la volatilidad disminuya....

Personalmente, creo que el patrón de conducta de la volatilidad hay que analizarlo con cuidado, las condiciones actuales del mercado no son las de hace 10 años, ahora hay muchas más "máquinas" con algoritmos que hacen sobre-reaccionar el mercado, para bien y para mal. Esta demostrado que las "máquinas" generan liquidez y reducen la volatilidad del mercado...cada algoritmo sigue una estrategia distinta y hay muchos que se agreden entre ellos, hasta siendo de la misma casa... pero esto es hablando en términos generales, cuando ocurre algo dramático y van todas en la misma dirección... se genera volatilidad... y mucha.

Espero que os ayude un poco....

Los Índices que siguen los ETP de Volatilidad

La prueba evidente de que la volatilidad a día de hoy es un activo de inversión como otro cualquiera: divisas, renta variable, commodities o renta fija, es que se emiten ETP que pueden ser suscritos por cualquiera, incluso particulares. Mayoritariamente los ETP que se emiten son ETN, aunque también hay algún ETF. Para los que no estéis familiarizados con las siglas anteriores, los Exchange Traded Products  o ETP son Productos Negociados en Bolsa, podéis ver aquí que son.

Es increible, pero la fama del VIX trasciende a los profesionales de los mercados financieros y prácticamente cualquier persona apenas iniciada en temas bursátiles conoce este índice. Lo cual, le convierte en el candidato ideal para emitir ETP sobre él. El inconveniente, es que los ETP suelen replicar el comportamiento de índices y el índice VIX no se puede replicar. Por esta razón, se han diseñado nuevos índices que invierten fundamentalmente en futuros de VIX que sí son replicables, pero son muy distintos del VIX y hay que conocer sus características. Existen muchos de todos los índices de volatilidad (VStoxx, Nasdaq, Russell, etc…) pero, sin ánimo de ser exhaustivos, mostraremos a continuación sólo algunos de los más relevantes referenciados al VIX:

• S&P500 VIX Short-Term Futures index.- Utiliza futuros de 1^er y 2º vencimiento. Va rolando la posición según van pasando los días en proporción a los días a vencimiento que quedan. Este índice también tiene la versión inversa.
• S&P500 VIX Mid-Term Futures index.- Utiliza futuros de 4º, 5º, 6º y 7º vencimiento. Igual que el anterior, va rolando proporcionalmente a los días.
• S&P500 VIX Enhanced Roll Futures index.- Este índice invierte en dos carteras: una a corto plazo que invierte en el índice Short Term y otra a medio plazo que invierte en el 3^er, 4º y 5º vencimiento. Por otro lado analiza una señal de la volatilidad implícita: si la volatilidad implícita es superior a 1.35 veces la media de los últimos 15 días la señal es positiva, si menor que 1.35 veces, pero está por encima de la media, la señal es cero y si está por debajo de la media la señal es negativa.  Según la señal sea positiva o negativa va invirtiendo en una u otra cartera, pero no lo hace de golpe, hace un 20% al día. Si la señal es positiva, es que la volatilidad está aumentando y como los vencimientos cortos son más sensibles,  tenderá a invertir en la cartera de corto plazo.  Si la señal es negativa, es que la volatilidad está bajando y como perjudica  a una posición larga, invertirá en la cartera de medio plazo que tiene menos volatidad..
• S&P500 Dynamic VIX Futures index.- Invierte en el índice Short-Term y en el índice Mid-Term y en función de la estructura temporal invierte unas cantidades determinadas en cada uno de ellos. La estructura temporal viene dada por la división entre VIX y VXV (93 días). No distingue más allá si la división es inferior al 90%  o superior al 115%.  Los rangos intermedios el asset allocation en cada índice está preestablecido.

En el gráfico 1, se puede observar el rendimiento de los índices anteriormente expuestos en comparación con el índice VIX, se observan diferencias evidentes y el daño que produce el rolo de la posición de futuros.

Gráfico 1: Comparativa de índices S&P sobre futuros de VIX con el índice VIX. Elaboración propia a partir de datos de SPindices y CBOE.

Para invertir en volatilidad, a continuación os digo los ETP más utilizados para cada tipo de índice.

Short Term:
iPath S&P 500 VIX ST Futures ETN (VXX)
ProShares VIX Short-Term Futures (VIXY)
VelocityShares VIX ST ETN (VIIX)

Mid Term:
iPath S&P 500 VIX MT Futures ETN (VXZ)

Apalancados:
ProShares Ultra VIX Short-Term Futures (UVXY)
VelocityShares Daily 2x VIX Short Term ETN (TVIX)

Inversos:
VelocityShares Daily Inverse VIX ST ETN (XIV)

ProShares Short VIX Short-Term Futures (SVXY)


Dynamic Futures:
iPath S&P 500 Dynamic VIX ETN (XVZ)

Enhanced Roll:

Lyxor ETF S&P 500 VIX Futures Enhanced Roll C-EUR VOOL
Lyxor ETF Unleveraged S&P 500 VIX Futures Enhanced Roll - C-EU ULVO 

Por último, y perdonad que sea insistente, pero si alguno de vosotros está pensado en invertir en volatilidad, tened en cuenta dos cosas: (1) la volatilidad de la volatilidad es muy elevada (2) elegid bien el ETN o ETF en función del índice que queráis seguir y utilizad este indice para seguir el comportamiento de vuestro producto, no el VIX.

Futuros del VIX

Hay futuros sobre el índice VIX y opciones sobre los futuros del VIX. Los futuros tienen la sorprendente peculiaridad de que no existe una relación de arbitraje con el índice VIX, puesto que éste no se puede replicar. El precio se forma por oferta y demanda.

Por lo demás, son futuros cuyas especificaciones no difieren de otro tipo de futuros. Tienen un multiplicador de 1000$, pero cambia en 0,01 puntos. Es decir de 16.10 a 16.11, por lo que el tamaño del tick es de 10$.

Los futuros vencen por diferencias (Cash Settelment). Los vencimientos son mensuales y son los miércoles que coincide 30 días antes del tercer viernes de vencimiento de las opciones del S&P 500 del mes siguiente. Normalmente coincide con el 3^er miércoles de vencimiento, salvo los meses de 5 semanas que será el 4º miércoles. Por ejemplo, el vencimiento de septiembre de 2014 fue el miércoles 17 de septiembre, dos días antes del vencimiento de las opciones del S&P500 que es el tercer viernes del mes. Sin embargo, el vencimiento de octubre fue el miércoles 22 de octubre de 2014 que es después del tercer viernes de octubre de 2014 y  justo 30 días antes del vencimiento de Noviembre que fue el 21 de noviembre de 2014.

La estructura temporal normal suele ser la de “Contango”, es decir, Base positiva. Cada vencimiento más lejano tiene más volatilidad, que es lo normal en la estructura temporal de la volatilidad. Cuando hay una caída súbita del mercado y aumenta mucho la volatilidad a corto plazo, la estructura cambia a Base negativa, “Backwardation”. Ver gráfico 1.

Gráfico 1: Precios de liquidación de los vencimientos del futuro de VIX a 6 de abril de 2015. elaboración propia.

Conocer esta estructura tiene mucha importancia, ya que como veremos en el siguiente "post" que voy a publicar, los productos de volatilidad en los que invierte la gente como ETF y ETN, siguen a índices que aunque tengan la palabra "VIX" por medio, no lo son. El índice VIX no es invertible, por tanto, se han elaborado otros índices que sí son invertibles y que están hechos con futuros. Por ejemplo el S&P500 VIX Short-Term Futures index, S&P500 VIX Enhanced Roll Futures index, etc. Obviamente los futuros se van rolando y la estructura temporal es muy importante.

Para una posición compradora de volatilidad, largo de futuro de VIX, el Roll-Over en “Contango” es costoso,  ya que se vende el futuro comprado a un precio bajo (futuro de Vto. cercano) y se vuelve a comprar a un precio alto (futuro de Vto. Lejano). En el gráfico 1 se observa que es mucho más costoso rolar de 1^er a 2º vencimiento (-1.85) que de 4º a 5º vencimiento (-0.25). Por esta razón hay índices que utilizan futuros cercanos y otros que utilizan vencimientos lejanos y el rendimiento de ambos difiere completamente.

Al contrario de lo anterior, una posición vendedora de volatilidad estaría ingresando cada vez que rolara. El problema es que la volatilidad es muy brusca y de repente, sencillamente “explota”. La posición vendedora puede haber estado generando mucho dinero recurrente durante semanas y en un solo día, perder todo. Con el agravante de que con la estructura en “Backwardation”, rolar le cuesta dinero.

Otros índices de volatilidad del VIX

Como el VIX solo está teniendo en cuenta volatilidades a 30 días, CBOE ha elaborado otros índices, con la misma metodología pero a diferentes plazos:

• CBOE Short-Term Volatility Index (VXST). Mide expectativas de volatilidad a 9 días. Utiliza opciones semanales. 
• CBOE 3-Month Volatility Index (VXV). Mide expectativas de volatilidad a 3 meses, más específicamente 93 días. 
• CBOE Mid-Term Volatility Index (VXMT). Mide expectativas de volatilidad a 6 meses. 

Combinando la información que ofrecen todos los índices anteriores, se puede obtener información muy valiosa de cómo evoluciona la estructura temporal de la volatilidad.

Como ya hemos comentado anteriormente en la estructura de volatilidad, los plazos cortos son mucho más volátiles que los largos..... lo mismo ocurre aquí. Aunque parezca un trabalenguas: "la volatilidad de la volatilidad es muy volátil", y cuanto más corto sea el plazo, más volátil.

En el siguiente gráfico podemos observar una comparativa de los índices anteriormente citados. Se aprecia a simple vista que la volatilidad es mayor cuanto más corto es el plazo. Específicamente en el periodo considerado (2011-abril 2015) las volatilidades han sido: VXST (181.68%), VIX (114.71%), VXV (71.05%) y VXMT (50.85%).

Metodología del cálculo del VIX

Para calcular el índice, se utilizan dos vencimientos de opciones uno que tiene que tener más de 23 días (near term) y otro que tiene que tener menos de 37 días a vencimiento (next term). Una vez a la semana se rola el índice a los vencimientos adecuados, incluye vencimientos mensuales y semanales. Luego se interpola ponderando por el tiempo las varianzas, tal y como vimos en la interpolación de la volatilidad en el tiempo, en la parte de "cálculos de volatilidad" En vez de utilizar precio negociados de las opciones, emplea el punto medio entre el Precio de compra (Bid) y de venta (Ask).

Una peculiaridad que no tiene más importancia, pero que merece la pena destacar es que para calcular el tiempo a vencimiento en años, se calcula teniendo en cuenta los minutos. Es necesario saber el tiempo que queda al vencimiento en años para el near y next term así como el tipo de interés asociado a cada plazo.

Una vez se conocen qué vencimientos se utilizan, el paso siguiente es seleccionar las opciones de la cadena de opciones disponible:

• Se seleccionan las opciones que estén cotizadas, si alguna no está cotizada (no tiene bid) no se selecciona y si hay dos precios de ejercicio seguidos sin cotización, ya no se siguen cogiendo más precios de ejercicio. Por esta razón, la cantidad de opciones empleadas varía casi constantemente.
• Se seleccionan precios medios entre Bid y Ask.
• Se restan Call y Put y dónde la diferencia sea mínima se calcula utilizando la paridad Call-put el precio del Futuro para cada vencimiento.
• El primer precio de ejercicio por debajo del futuro es el precio de ejercicio ATM. Teniendo en cuenta este precio de ejercicio ATM, se seleccionan los precios de los Put OTM (precio de ejercicio menor que el ATM) y los Call OTM (precio de ejercicio superior al ATM). Para el precio de ejercicio ATM se utiliza el promedio del precio de Call y Put.

El siguiente paso sería calcular la volatilidad con la siguiente fórmula:

Se observa en la fórmula anterior que cada precio de la opción Q(K_i) está ponderado por el salto del precio de ejercicio dividido por el precio de ejercicio al cuadrado (DK/K²). Ésta es la contribución de cada precio de ejercicio. Este salto de precio de ejercicio depende de las opciones seleccionadas. Se selecciona el precio de ejercicio inmediatamente inferior y superior y se haya el promedio, coincidirá con el salto de cada precio de ejercicio excepto cuando no se haya seleccionado algún precio de ejercicio por no tener precios.

Una vez calculadas las dos varianzas, se halla la Raíz de la media ponderada por tiempo y se multiplica por 100, ya que el VIX viene expresado en números enteros, es decir, una volatilidad anual del 20% es 20.

Para ver un ejemplo completo del cálculo, se recomienda leer VIX White en la página web de CBOE.

Historia del VIX

Una vez que hemos visto un poco cómo se pueden tomar posiciones de volatilidad a través de opciones y Variance Swaps, en las siguientes entradas voy a explicar cómo invertir en volatilidad a través de futuros y ETPs sobre índices de volatilidad. ¡Mucho cuidado con estos índices! hay gente que está muy equivocada, creyendo que sigue un índice muchas veces está siguiendo otro. Pero no me voy a adelantar.... hoy me gustaría empezar explicando brevemente qué es el VIX y un poco de su historia.

Lo primero que hay que saber, es que se trata del Índice de volatilidad implícita de las opciones del índice S&P 500 de 30 días a vencimiento, es conocido como el “indicador del miedo” que existe en el mercado. Es calculado cada 15 segundos. Al ser la volatilidad implícita, no realizada, son expectativas de volatilidad, y por tanto reflejan la incertidumbre del mercado. Por esta razón es ampliamente seguido en los mercados financieros. Como ya hemos visto anteriormente en alguna ocasión, tiene una alta correlación negativa con el índice S&P 500. Lo comentaremos más adelante, pero también es muy importante saber que no se puede invertir en él, es decir, NO HAY NINGÚN producto que siga exactamente al VIX, ¡tampoco sus futuros!

El primero en proponer un índice de volatilidad fue Robert Whaley, en 1993 con su artículo “Derivatives on Market Volatility: hedging tools long overdue” publicado en el  Journal of Derivatives.

Originariamente, en 1993,  el VIX era calculado con opciones sobre el índice S&P 100 que eran las más líquidas en ese momento. En el año 2003 hubo un cambio de metodología con dos grandes cambios:

1. El Nuevo método obtiene la volatilidad de un rango muy amplio de opciones del S&P 500 (todos los strikes posibles), no sólo de las opciones ATM. Además no utiliza ningún modelo de valoración de opciones para despejar la volatilidad implícita. Pondera el precio de las opciones OTM por la amplitud del salto del precio de ejercicio divido por el precio de ejercicio al cuadrado y calcula la varianza de los precios. De esta manera recoge información del Skew. Método simple y potente.
2. No utiliza las opciones del índice  S&P100 (OEX) sino las del índice S&P500 (SPX).

El índice VIX original sobre las opciones del índice S&P100 se sigue calculando bajo el nombre VXO. En el Gráfico 1 podemos observar que las diferencias entre una y otra metodología, se puede apreciar que tampoco existen unas diferencias excesivamente significativas.

Volatilidad IBEX 35 Mayo 2015

Hola a todos,

No es normal que haga dos entradas tan seguidas en el Blog, pero quiero distinguir las entradas que son puramente formativas, explicando pequeños conceptos financieros de otras entradas sobre la situación actual de la volatilidad del IBEX 35, hace mucho que no las hago y probablemente sea de las que más gustan...

En primer lugar comentar como siempre que con el análisis de la volatilidad se pueden tomar conclusiones que ayuden a la gestión de las posiciones, no solo a invertir en volatilidad.

En primer lugar os quiero poner un gráfico desde al año 2005 donde podéis tener una visión más amplia de lo que está ocurriendo a la volatilidad. Por supuesto, hay determinadas situaciones que no son extrapolables a la situación actual. Quiero decir, esos picos de volatilidad del año 2008, 2010, 2011 y 2012 no tienen porqué necesariamente volver a repetirse en el corto plazo, pero queda claro que estamos en volatilidades históricamente bajas, que es lo que suele ocurrir cuando los mercados son alcistas.

Si analizamos en detalle el año 2015, vemos que hay un punto claro de cruce de la volatilidad a corto plazo (20s) por debajo de la volatilidad a largo plazo (60s) lo que indica cambio de tendencia en volatilidad y que esta disminuyendo. Por otro lado vemos en el otro extremo el gráfico varios cruces de las medias que responden a las caídas fuertes y posteriores rebotes de las últimas semanas. En este contexto macro de incertidumbre, es difícil predecir si se está formando un rebote de la volatilidad, pero todo pinta a que es así, y por tanto habría que estar muy atento.

Ahora un par de gráficos que vienen a dar más o menos la misma información sobre los que hemos hablado en anteriores ocasiones. Si no entendéis de lo que os hablo, id a las entradas de superficies y de la dinámica del skew 

El primero es la Superficie de volatilidad de las opciones de IBEX 35 de ayer. Fijaros en el Skew de primer vencimiento (mayo) que está bastante empinado y es más elevado que las opciones de Marzo 16.

 En el gráfico de Skew, se observa perfectamente el gráfico invertido, las opciones de mayo tienen más volatilidad.

Con volatilidades implícitas ATM en los entornos del 25% cuando las históricas están en el 20% y subiendo....me puedo equivocar, pero todo apunta a un próximo repunte de volatilidad...

Cobertura Delta y el Gamma Scalping

Otra manera de tomar una exposición a la volatilidad, es mediante opciones, se compran o venden y se cubre la delta para no tener exposición direccional, sólo a la volatilidad. Esto se llama cobertura Delta Neutral.

Gamma Scalping se conoce al ajuste que se hace con el activo subyacente para rebalancear la cobertura delta neutral y mantener una exposición a la volatilidad sin tener exposición al activo subyacente.

El mayor beneficio/pérdida por el Scalping Gamma lo haremos en las opciones ATM y de vencimiento más corto, ya que son las que más Gamma tienen, y a poco que se mueva el activo subyacente cambiará mucho la Delta de la opción. Cuanto más cambie la Delta, más infravalorará la cobertura Delta en la cobertura de opciones compradas (Gamma positivo). ¿Cuánto? La cantidad dependerá de la diferencia entre la Delta inicial y final, que es Gamma x DS, donde DS es el cambio del activo subyacente. Si asumimos que Gamma es constante (la realidad es que varía muy poquito), lo que gana o pierde de valor la opción será el promedio de Delta.

Por otro lado, lo que gana o pierde la cobertura Delta es la Delta inicial, por tanto la diferencia entre ambas será ½ de Gamma x DS.

Para más detalle, ver el polinomio de Taylor que nos ayuda aproximar y ver también el Lemma de Itô , ya que podemos considerar el Lemma de Itô como un caso particular de Taylor. Todos  los cálculos que se hacen utilizando el Polinomio de Taylor son aproximados, ya que habría que incorporar el efecto del paso del tiempo y volatilidad.

El resumen del Bº/Pª a través del Gamma Scalping se puede resumir en el siguiente gráfico.

Efecto Convexidad de un Variance Swap

Aunque el pago a vencimiento de un Variance Swap es lineal respecto de la varianza, es convexo respecto de la volatilidad.

El nocional en términos de Vega representa la ganancia o pérdida media por cada 1% de movimiento de la volatilidad. De esta manera, una posición larga se beneficia más ante aumentos de volatilidad y pierde menos ante caídas en la volatilidad. Lo contrario le ocurre a las posiciones cortas. Lo anterior podemos verlo en el gráfico 1 donde se compara el Variance Swap con un Volatility Swap.

Gráfico 1: Efecto convexidad de un Variance Swap de 68.000 de Vega notional y un Strike de 17.

Este efecto convexidad es el que hace que el Strike del Variance Swap esté ligeramente por encima de la volatilidad ATM al mismo plazo (un volatility Swap), este hecho es amplificado por el Skew de volatilidad existente. Si un Volatility Swap y un Variance Swap tuvieran el mismo Strike, se podrían arbitrar. Por ello, habitualmente para hacer un cálculo rápido y aproximado, se considera como Strike del Variance Swap la volatilidad del Put 90% (un 10% por debajo del precio del activo subyacente, lo que suele coincidir más o menos con una delta del Put del 30%).

Variance Swap y su pago a vencimiento.

Ya sabemos que la volatilidad es una característica de las inversiones, a mayor volatilidad mayor riesgo y viceversa. Por eso se mide la volatilidad, para medir el riesgo. Sin embargo, de unos años a esta parte, se ha convertido en un activo en sí mismo, en el que se puede invertir y que tiene propiedades muy interesantes. Vamos a explicar en los próximos artículos cómo podemos invertir en volatilidad. Cuando los haya hecho todos, los pasaré agrupados a la sección de "Invertir en volatilidad".

En primer lugar, explicaremos qué es un Variance Swap, es una alternativa muy profesional que no está al alcance de todos, pero poco a poco llegaremos a otras alternativas más accesibles para cualquiera, como son los futuros o los ETP.

Un Variance Swap es un instrumento OTC que otorga una exposición directa a la volatilidad realizada futura, aunque para ser más precisos, es la varianza realizada futura. Como todos los Swap es una permuta, pero en este caso las partes acuerdan intercambiar la volatilidad realizada durante un periodo de tiempo por un nivel fijado al principio de la vida del Swap, que se denomina Strike.

El Variance Swap ofrece exposición directa a la volatilidad realizada sin los problemas de path dependency de la Cobertura Delta Neutral y su Gamma Scalping. Hablaremos en otro artículo de ello, tan sólo tenéis que saber de momento que, por  ejemplo, en una cobertura delta neutral si estamos largos de volatilidad y efectivamente la volatilidad aumenta, los beneficios que se generen dependen de cómo se realice esa volatilidad, incluso puede que no haya beneficios.

En un Variance Swap, se fija el Strike de manera que no haya que pagar nada al principio, como sucede con todos los Swaps. Por convención  se cotiza en unidades de volatilidad, pero el pago se mide en términos de varianza. 

El Beneficio/Pérdida a vencimiento (pay off) de una posición compradora se determina por la diferencia entre  la varianza realizada durante la vida del Swap y Strike.

El nocional del Swap se puede expresar en unidades de Varianza o en unidades de Vega (Volatilidad). El Bª/Pª se calcula utilizando unidades de varianza, pero debido a que la varianza está expresada en puntos porcentuales al cuadrado que es más difícil de interpretar, por convención de mercado es habitual hablar en unidades de volatilidad (Vega). También por convención se omite el porcentaje y no se habla de volatilidad del 25% sino de 25.

El nocional en términos de Vega, representa aprox. el Bª/Pª por cada 1% (una Vega) de movimiento de la volatilidad, es decir, pasar por ejemplo de 25 a 26. 

Pongamos un ejemplo. Supongamos que se ha comprado un Variance Swap de Euro Stoxx 50 con un Strike de 17 con un Variance Notional de 2,000. El Vega Notional es de 68,000.

Vega Notional= Variance Notional  (2 x K)= 2,000 x (2 x 17)=68,000€

Si el índice  Euro Stoxx 50 realiza una volatilidad de 14 o de 21 daría lugar al siguiente Bº/Pª:

• Volatilidad realizada de 14%:

68,000€ x ((14²-17²)/(2x17))=-186,000€ de pérdida.

 Si se calcula en términos de Variance Notional: 2,000 x(14²-17²)=-186.000€

• Volatilidad Realizada del 21%:

68,000€ x ((21²-17²)/(2x17))=304,000€ de beneficio.

Si se calcula en términos de Variance Notional: 2,000 x(21²-17²)=304.000€

Ejemplo Numérico Sensibilidades

Hola a todos,

El otro día, a consecuencia del artículo de Vanna y Volga, recibí un comentario de Pedro Enrique Blanque Amorós diciéndome que podría hacer un "ejemplito" numérico que haría más visibles las fórmulas.... y la verdad es que me gustó mucho el comentario, yo también soy de ponerle números a las cosas para "aterrizarlas", y ya que me pongo... pues voy a hacer todas las sensibilidades.

En primer lugar un pongo una imagen de un excel que es una calculadora de opciones con todos los cálculos (Black-Scholes), por si alguno quiere replicar los ejemplos que vamos a ver a continuación. Al utilizar entorno de valoración Black-Scholes-Merton, está claro que son opciones europeas.

Delta: Mide el cambio en el precio de la opción (Prima) ante cambios en el activo subyacente.
Gamma: Mide cuánto varía Delta antes cambios en el activo subyacente.
Theta: Mide cuánto varía el precio de la opción (prima) antes variaciones en el tiempo. El paso de un día.
Vega: Mide cuánto varía el precio de la opción (prima) antes variaciones en la volatilidad de un 1%.
Rho: Mide cuánto varía el precio de la opción (prima) antes variaciones en los tipos de interés.
Volga: Mide cuánto varia Vega ante cambios en la volatilidad implícita.

Vanna: Mide cuánto varía Vega ante variaciones en el activo subyacente o delta ante cambios en la volatilidad implícita.

Como podéis apreciar en el cuadro anterior tenemos el activo subyacente en 100 y el precio de ejercicio es también 100. Quedan 60 días al vencimiento (0,16 años, que es lo que utiliza la fórmula), la volatilidad es del 20% y los tipos de interés en el 1,1% y dividendos están en el 1%.

Si sube el activo subyacente a 101.

La prima de un Call pasa de valer 3,259 a 3,800, es decir una diferencia de 0,54. Ya que delta es la primera derivada (pendiente) y gamma es la segunda derivada (convexidad), no sólo podemos tener en cuenta delta, ya que estaremos cometiendo un pequeño error de convexidad.
Si la prima de Call le añadimos Delta x movimiento+(Gamma x movimiento^2)/2 es decir, 3,259+(0,516x1)+(0,049x1^2)/2=3,800.
La delta pasa de valer a 100 0,516 a valer 0,564 en 101 (la diferencia son esos 0,049 aprox, ya que hay redondeos)
La gamma varía ligeramente, pero también hay cambios en el resto de sensibilidades.

Si pasa un día

La prima del Call pasa de 3,259 a 3,232 es decir un -0,027€ euros menos, que es exactamente la Theta que tenemos en la imagen superior. Habitualmente viene expresada ya en euros. Como en el caso anterior, también varían el resto de sensibilidades.

Si aumenta o disminuye la volatilidad implícita un 1%

En este caso, hace falta aplicarle la tasa de cambio. Si sube la volatilidad al 21% el precio de la opción varía de 3,259 a 3,422 cuyo cambio son los 16,245 que nos indica Vega multiplicados por 0,01 (1%).

Por otro lado, Vega varía de 16,245 a 16,243, realmente, teniendo en cuenta algunos decimales más de 16,244697 a 16,243312, es decir que ha variado -0,001384 que es precisamente Volga multiplicado por 0,01.

Delta también ha variado de 0,516 a 0,517, nuevamente si utilizamos más decimales de 0,5162347 a 0,5170082, ha variado 0,00077, que es Vanna multiplicado por 0,01

Si aumenta o disminuye los ti en 1%

En este caso, al igual que en anterior, hay que aplicar el cambio. La opción pasa de valer 3,259 a 3,34, un 0,0812 que el valor que teníamos de Rho multiplicado por 0,01.

Espero que os sirva. El artículo es un "pelín" más denso de lo que suelo hacer, pero efectivamente la única manera de aterrizar las sensibilidades es cogiendo la hoja de cálculo e ir variando parámetros y estudiar sus efectos. Por esta razón, recomiendo intentéis replicar en vuestro excel la imagen que os pongo en este artículo.

Vanna y Volga

Vamos a introducir dos sensibilidades de opciones que por ser más específicas de posiciones en volatilidad y skew, no suelen ser tan conocidas como: Delta, Gamma, Vega, Theta y Rho, pero que resultan de utilidad.

Volga y Vanna, aunque parezcan los nombres de letras griegas, en realidad no lo son, al igual que Vega que no es una letra del alfabeto griego clásico. Por eso a mi me gusta utilizar el término sensibilidades, no griegas.

Volga

Es la gamma de la volatilidad (VOLatility GAmma). Expresa los cambios en Vega ante cambios en la volatilidad implícita.

Es muy elevada para opciones que están fuera del dinero (aproximadamente Delta 10%). Ver gráfico 1.

Gráfico 1: Volga de un Call de IBEX precio de ejercicio 10.800. El activo subyacente está a 10.736 y la volatilidad en el 26%.

Igual que una posición con Gamma positivo se benéfica de la volatilidad del activo subyacente, Volga se beneficia de la volatilidad de la volatilidad. Se puede calcular la volatilidad de la volatilidad igual que si se calculara del activo subyacente.

Vanna

Formalmente, extraída de la fórmula de Black-Scholes, al igual que hemos hecho con Volga es:

Tiene dos definiciones o interpretaciones:

• Cambio en Vega ante variaciones en el activo subyacente: 

• Cambio en delta ante cambios en la volatilidad implícita: 

El cambio en Vega ante cambios en el precio del activo subyacente (Spot), es la pendiente de vega. Puede ser considerado como la medición del tamaño del Skew de la posición. Un risk reversal o túnel vendido por ejemplo (compra de Put precio de ejercicio bajo y venta de Call precios de ejercicio alto) se beneficiará de caída en el activo subyacente y de un empinamiento del skew. Es positiva para caídas del activo subyacente y negativo para aumentos de éste.

Gráfico 2: Vanna de un Call de IBEX precio de ejercicio 10.800. El activo subyacente está a 10.736 y la volatilidad en el 26%.

Superficie de volatilidad

En las dos últimas entradas hemos hablado de la estructura temporal y el skew de volatilidad, de cómo reaccionan ante un "Shock" del mercado. He estado refiriéndome a dos fechas: una el 9/10/14 y otra el 12/1/15 por ser dos momentos muy diferentes. Uno en el que el mercado está en relativa tranquilidad (principios de octubre del 2014) y otro en el que está en plena reacción de diferentes acontecimientos (enero de 2015) que afectan al mercado: Rusia y su rublo, Grecia, Ucrania, etc...

Pues bien, si se unen en el mismo gráfico los dos anteriores (skew y estructura temporal), es el gráfico que denominamos superficie de volatilidad.

En el gráfico 1 se representan la superficie de volatilidad normal. Al ser "3d" cuesta un poquito de entender al principio, pero nos acostumbramos a él, no ofrece muchísima información de un sólo vistazo. Si os fijáis detenidamente, deberíais poder distinguir lo que habíamos comentaedo en anteriores entradas, el Skew de opciones a más corto plazo es más empinado que las opciones a largo plazo. Por otro lado la volatilidad de los plazos más largos es más alta, salvo para los precios de ejercicio bajos de vencimientos cercanos.

Gráfico 1: Superficie de volatilidad de normal

La superficie de volatilidad permite hacer un análisis mediante el cual podemos estimar la dinámica del cambio de la volatilidad a lo largo de los strikes y de los distintos vencimientos. Así por ejemplo, en el gráfico 2 se observa cómo en un plazo de varias semanas, la superficie de volatilidad ha variado sensiblemente.

En representado la superfice de volatilidad del 9/10/14 y la del 12/1/15 en el mismo gráfico para que podáis apreciar el movimiento que ha hecho la superficie de volatilidad. Sé que es difícil de apreciar, pero si te fijas detenidamente, te darás cuenta de que sucede lo que habíamos comentado en las anteriores dos entradas: la volatilidad a corto plazo reacciona muy fuerte, hay un movimiento muy fuerte hacia arriba y el skew se aplana levemente (los precios de ejercicio bajos son más "sticky"). La volatilidad a más largo plazo es más "sticky" y el aumento es mucho más pequeño.

Gráfico 2: modificación de la superficie de volatilidad entre el 9/10/14 (color azul) y 12/01/15 (color rojo).

Espero que os haya gustado. Os adelanto que las próximas entradas del blog serán los modelos de la dinámica de la superficie de volatilidad: Sticky strike, sticky delta, etc...

Dinámica del SKEW ante una caída fuerte del mercado

Ya hemos comentado en alguna ocasión que el skew de volatilidad en mercados de renta variable suele ser decreciente y más empinado para volatilidades a corto plazo que a largo plazo, tal y como se puede apreciar en el gráfico 1.

Gráfico 1: Skew de volatilidad para opciones de distintos vencimientos.

Fijaros en el gráfico anterior como el Skew a 3 meses está muy empinado mientras que el Skew de opciones de vencimiento 4 años, está bastante más plano.

Cuando hay una caída fuerte en el activo subyacente, es razonable pensar en un fuerte aumento de la volatilidad realizada. Por tanto, precios de ejercicio por debajo del subyacente y opciones a largo plazo ( ver el artículo de estructura temporal) que ya tenían una volatilidad implícita más elevada, aumentarán menos que precios de ejercicio ATM y plazos más cortos. Se suele decir que opciones de precios de ejercicio bajos y vencimientos largos tienen la volatilidad “sticky” (pegajosa), es decir que cambia menos. Esto hace que el dato de Skew por si mismo no sea un indicador de riesgo muy fiable, ya que es habitual que la diferencia entre precios de ejercicios bajos y ATM suele ser más grande cuando disminuye la volatilidad implícita. Por ello es importante observar la dinámica de comportamiento del Skew.

Como sabéis, me gusta poner siempre situaciones reales, veamos un par de ejemplos. En los Gráficos 2 y 3 podemos observar este efecto.

En el gráfico 2 tenemos los skew de opciones de IBEX 35 a diferentes plazos del día 9 de octubre de 2014, en un momento de tranquilidad en el mercado. El skew de corto plazo está bastante empinado, mientras que las opciones a más largo plazo tienen menos pendiente

Gráfico 2: Skew de opciones de IBEX 35 el día 9 de octubre de 2014

En gráfico 3 tenemos los mismos gráficos de opciones de IBEX 35 pero el 12 de enero de 2015, momento bastante volátil, dónde observa que las volatilidades de todos los precios de ejercicio han aumentado, pero lo han hecho de diferente manera. Fijaros como en general hay menos pendiente (120%-80%) en todos los plazos, las que más han reaccionado han sido las de más corto plazo (3 meses y 6 meses) mientras que el Skew de opciones a más largo plazo casi no ha variado. Éstos son más “sticky”.

Gráfico 3: Skew de opciones de IBEX 35 el día 12 de enero de 2015